如何创造可信任的机器学习模型？先要理解不确定性

在谈到人工智能安全、风险管理、投资组合优化、科学测量和保险时，人们都会提到「不确定性(uncertainty)」的概念。下面有几个人们言语中涉及不确定性的例子：

「我们想让机器学习模型知道它们不知道的东西。」

「负责诊断病人和给出治疗方案的 AI 应该告诉我们它对自己的推荐的信心。」

「科学计算中的显著性值代表了测量中的不确定性。」

「我们想让自动智能体探索它们不确定(对于奖励或预测)的区域，这样它们也许能发现稀疏的奖励。」

「在投资组合优化中，我们希望最大化回报，同时限制风险。」

「由于地缘政治不确定性增大，美国股市 2018 年在失望中收尾。」

那「不确定性」究竟是什么?

不确定性度量反映的是一个随机变量的离散程度(dispersion)。换句话说，这是一个标量，反应了一个随机变量有多「随机」。在金融领域，这通常被称为「风险」。

不确定性不是某种单一形式，因为衡量离散程度的方法有很多：标准差、方差、风险值(VaR)和熵都是合适的度量。但是，要记住一点：单个标量数值不能描绘「随机性」的整体图景，因为这需要传递整个随机变量本身才行!

尽管如此，为了优化和比较，将随机性压缩成单个数值仍然是有用的。总之要记住，「越高的不确定性」往往被视为「更糟糕」(除了在模拟强化学习实验中)。

不确定性的类型

统计机器学习关注的是模型 p(θ|D) 的估计，进而又估计的是未知随机变量 p(y|x)。其中有多种不同形式的不确定性。某些不确定性的概念描述了我们能够预期的固有的随机性(比如抛硬币的结果)，另一些概念则描述了我们对模型参数的最佳猜测的信心缺乏程度。

为了说得具体一点，我们假设有一个循环神经网络(RNN)需要根据一个每日气压表读数序列预测当天的降雨量。气压表能检测大气压，大气压下降往往是降雨的前兆。下图总结了降雨量预测模型与不同类型的不确定性。

图 1

图 1：试图根据气压表读数序列预测每日降雨量的简单机器学习模型可能考虑的不确定性。偶然事件不确定性(Aleatoric Uncertainty)源自数据收集过程，是不可降低的随机性。认知不确定性(Epistemic Uncertainty)反映的是模型做出正确预测的置信程度。最后，超出分布的误差(Out-of-Distribution error)是指当模型的输入不同于其训练数据时出现的不确定性(比如太阳温度等其它异常现象)。

偶然事件不确定性

偶然事件不确定性得名于拉丁语词根 aleatorius，意为「将几率纳入创造过程」。这描述的是源自数据生成过程本身的随机性;不能简单地通过收集更多数据而消除的噪声。就像你不能预知结果的抛硬币。

在降雨量预测的类比中，偶然事件不确定性源自气压表的不准确度。也还存在这种数据收集方法没有观察的重要变量：昨日的降雨量是多少?我们测量大气压的时代是现代还是上个冰河时代?这些未知是我们的数据收集方法中固有的，所以用该系统收集更多数据无法帮助我们消除这一不确定性。

偶然事件不确定性会从输入传播到模型的预测结果。假设有一个简单模型 y=5x，它的输入取自正态分布 x∼N(0,1)。在这一案例中，y∼N(0,5)，因此该预测分布的偶然事件不确定性可描述为 σ=5。当然，当输入数据 x 的随机结构未知时，预测结果的偶然事件不确定性将更难估计。

也许有人会想：因为偶然事件不确定性是不可约减的，所以我们对此无能无力，直接忽略它就好了。这可不行!在训练模型时，应该注意选择能够正确地代表偶然事件不确定性的输出表征。标准的 LSTM 不会得出概率分布，所以学习抛硬币的结果时只会收敛成均值。相对而言，用于语言生成的模型能够得出一系列类别分布(词或字符)，这能纳入句子完成任务中的固有歧义性。

认知不确定性

「好的模型都是相似的;差的模型各有不同。」

认知不确定性来自希腊语词根 epistēmē，属于与知识相关的知识。这衡量了我们对「源自我们对正确模型参数的无知程度」的正确预测的无知程度。

下图展示了一个在某个简单的一维数据集上的高斯过程回归模型。其置信区间反映了认知不确定性;训练数据的认知不确定性为零(红点)。随着我们离训练数据点的距离越远，模型应该给预测分布分配越高的标准差。不同于偶然事件不确定性，认知不确定性可以通过收集更多数据和「去除」模型缺乏知识的输入区域而降低。

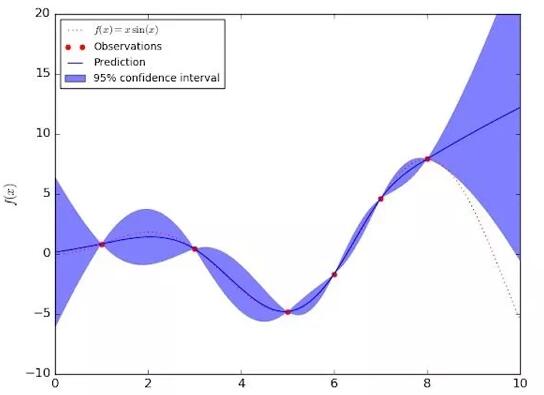
图 2：一维高斯过程回归模型，展现了训练集之外的输入上的认知不确定性