拜托，面试别再问我TopK了！！！

面试中，TopK，是问得比较多的几个问题之一，到底有几种方法，这些方案里蕴含的优化思路究竟是怎么样的，今天和大家聊一聊。

画外音：除非校招，我在面试过程中从不问TopK这个问题，默认大家都知道。

问题描述：从arr[1, n]这n个数中，找出最大的k个数，这就是经典的TopK问题。

栗子：从arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 这n=12个数中，找出最大的k=5个。

一、排序

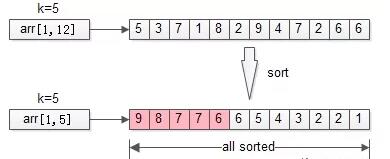
排序是最容易想到的方法，将n个数排序之后，取出最大的k个，即为所得。

伪代码：

sort(arr, 1, n); 

return arr[1, k]; 

时间复杂度：O(n*lg(n))

分析：明明只需要TopK，却将全局都排序了，这也是这个方法复杂度非常高的原因。那能不能不全局排序，而只局部排序呢?这就引出了第二个优化方法。

二、局部排序

不再全局排序，只对最大的k个排序。

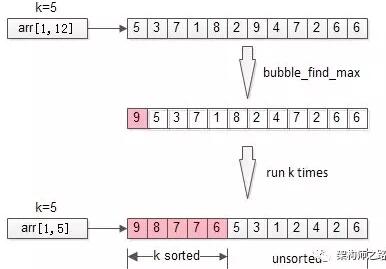
冒泡是一个很常见的排序方法，每冒一个泡，找出最大值，冒k个泡，就得到TopK。

伪代码：

for(i=1 to k){ 

         bubble_find_max(arr,i); 

} 

return arr[1, k]; 

时间复杂度：O(n*k)

分析：冒泡，将全局排序优化为了局部排序，非TopK的元素是不需要排序的，节省了计算资源。不少朋友会想到，需求是TopK，是不是这最大的k个元素也不需要排序呢?这就引出了第三个优化方法。

三、堆

思路：只找到TopK，不排序TopK。

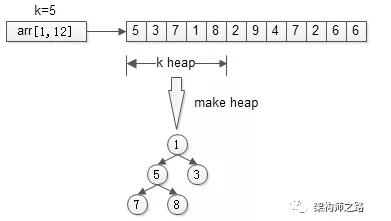
先用前k个元素生成一个小顶堆，这个小顶堆用于存储，当前最大的k个元素。

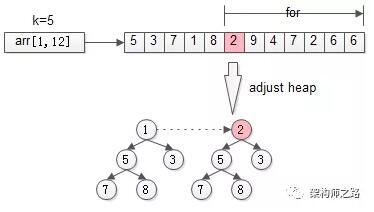
接着，从第k+1个元素开始扫描，和堆顶(堆中最小的元素)比较，如果被扫描的元素大于堆顶，则替换堆顶的元素，并调整堆，以保证堆内的k个元素，总是当前最大的k个元素。

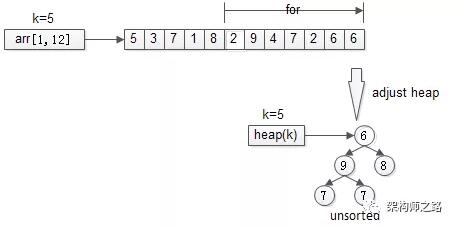
直到，扫描完所有n-k个元素，最终堆中的k个元素，就是猥琐求的TopK。

伪代码：

heap[k] = make_heap(arr[1, k]); 

for(i=k+1 to n){ 

         adjust_heap(heep[k],arr[i]); 

} 

return heap[k]; 

时间复杂度：O(n*lg(k))

画外音：n个元素扫一遍，假设运气很差，每次都入堆调整，调整时间复杂度为堆的高度，即lg(k)，故整体时间复杂度是n*lg(k)。

分析：堆，将冒泡的TopK排序优化为了TopK不排序，节省了计算资源。堆，是求TopK的经典算法，那还有没有更快的方案呢?

四、随机选择

随机选择算在是《算法导论》中一个经典的算法，其时间复杂度为O(n)，是一个线性复杂度的方法。

这个方法并不是所有同学都知道，为了将算法讲透，先聊一些前序知识，一个所有程序员都应该烂熟于胸的经典算法：快速排序。

画外音：

如果有朋友说，“不知道快速排序，也不妨碍我写业务代码呀”…额...

除非校招，我在面试过程中从不问快速排序，默认所有工程师都知道;

其伪代码是：

void quick_sort(int[]arr, int low, inthigh){ 

         if(low== high) return; 

         int i = partition(arr, low, high); 

         quick_sort(arr, low, i-1); 

         quick_sort(arr, i+1, high); 

} 

其核心算法思想是，分治法。